Linear Regression

Comments

Goal

This post aims to introduce linear regression using dummy data.

image

Reference

Libraries

In [3]:
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
%matplotlib inline

Create dummy linear data

Let's create 1-dimensional $\mathbf{y}$ data which has the linear relationship based on the following equations:

\begin{equation*} \mathbf{y} = \mathbf{A}\mathbf{x} + \mathbf{b} + \mathbf{e} \end{equation*}

Here $\mathbf{x}$ is 1 dimension data, $\mathbf{b}$ is constant, $\mathbf{e}$ is white noise.

In [9]:
a = 10
b = 4
n = 100
sigma = 3
e = sigma * np.random.randn(n) 
x = np.linspace(-1, 1, num=n)
y = a * x + b + e
In [10]:
plt.plot(x, y, '.', label='observed y');
plt.plot(x, a * x + b, 'r', label='true y');
plt.legend();

Fitting

Now we can see how the coefficient A and the intercept b are close to the ones I used to create this dataset.

In [13]:
reg = LinearRegression()
reg.fit(x.reshape(-1, 1), y);
In [14]:
print(f'Coefficients A: {reg.coef_[0]:.3}, Intercept b: {reg.intercept_:.2}')

Coefficients A: 9.01, Intercept b: 3.7
In [23]:
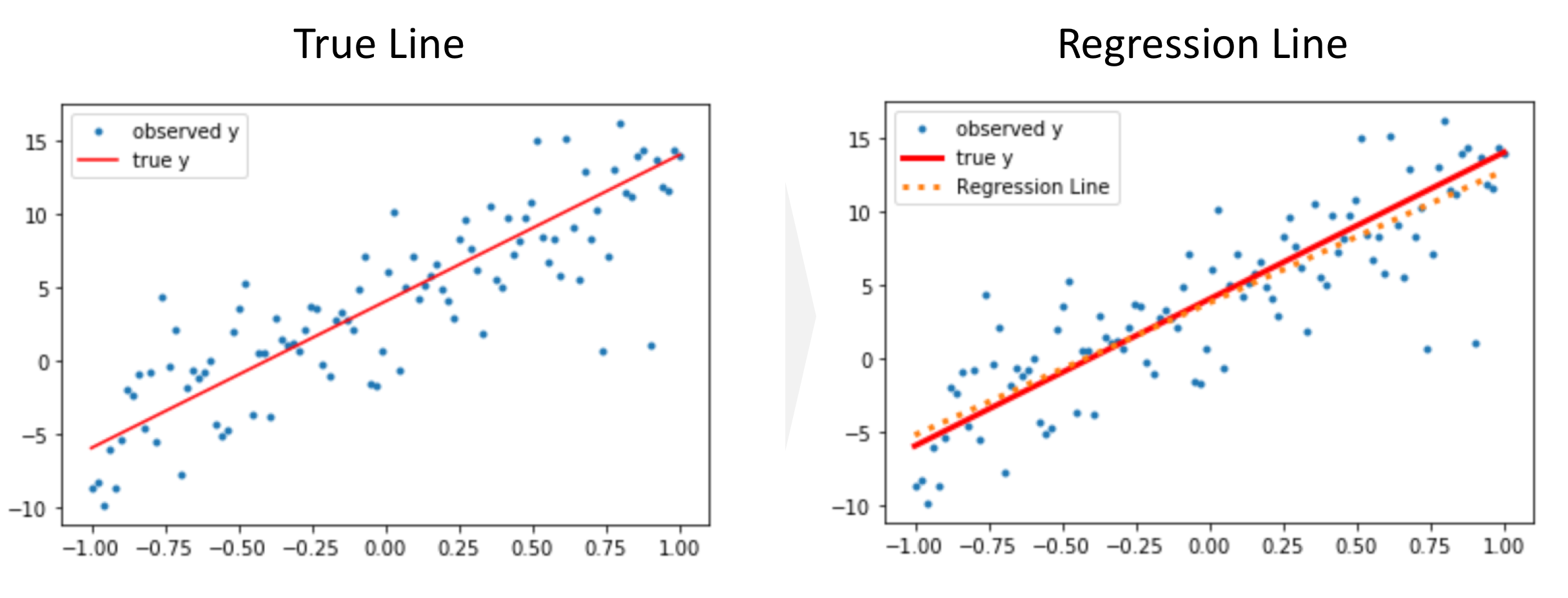
plt.plot(x, y, '.', label='observed y');
plt.plot(x, a * x + b, 'r', label='true y', lw=3);
plt.plot(x, reg.coef_[0] * x + reg.intercept_ , label='Regression Line', c='C1', ls='dotted', lw=3)
plt.legend();
plt.title('Regression Lines');

Comments

Comments powered by Disqus